Для чего Эрнё Рубик придумал кубик 3х3?

История математики кубика Рубика

Трудно найти того, кто не знает головоломки кубик Рубика. Даже те, кто не умеют её собирать, прекрасно знают о её популярности. Но как она приобрела такую славу, и зачем вообще создавалась? В этой статье я расскажу понятным и веселым языком о своем маленьком расследовании на эту тему, проходящее через глубины математики, а также истории и немного инженерии.

Ходят много разных баек, как и зачем Эрнё Рубику, венгерскому профессору архитектуры, пришла в голову идея создать 26 подвижных блоков, образующих кубическую головоломку. Это чем-то похоже на историю с Ньютоном: никто не знает, действительно ли ему на голову падало это злосчастное яблоко, или он просто думал о том, что общего между падающим ему на голову яблоком и вращающейся луной, благодаря чему и открыл свой закон. Можно было бы спросить самого Ньютона, но, к сожалению, это вряд ли бы дало нам какую-то более точную информацию – Ньютон нам уже не ответит, и нам остается только гадать.

И тем не менее, некоторые вещи о создании кубика Рубика мы можем утверждать точно.

1.Еще до изобретения кубика были аналоги игрушек-головоломок, которые тогда воспринимались как что-то математическое, нежели попсовое, и с которых Эрнё взял пример. Уже существовала магнитная версия кубика 2х2 без механизма крестовины внутри кубика, как это привычно нам сейчас. Также рассматривались идеи о перенесении пятнашек на магнитную сферу (кстати одна из таких есть в магазине: https://cubemarket.ru/products/yuxin-12-hole-rainbow-ball). Чуть позже параллельно с Рубиком была изобретена пирамидка Мефферта… да-да, пирамидка Рубика – это не пирамидка Рубика, - официально это пирамидка Мефферта =)

Более того, Рубик не получает деньги со всех продаж всех кубиков в мире, даже если брать только его обычный кубик Рубика 3х3. Дело в том, что технически то, что мы покупаем в магазинах – это аналоги, созданные для скоростных соревнований, и технически предназначенное для детей постарше. Компания же Rubik’s ставит одной из первостепенных задач прочность игрушек, так как играть в них могут все – от бабушек до маленьких детей. Так что головоломок полно даже без Рубика, хотя он и был одним из основоположников.

2.Эрнё задумал свою головоломку вовсе не как головоломку, и уж тем более, не как средство для массового получения денег, — это было просто наглядным пособием для студентов, которым он никак не мог втолковать Теорию Групп. Когда он принес готовую модель для пробы, оказалось, что простую затею не так-то просто решить, и у самого профессора, при всей его математической подготовке, ушел целый месяц на изобретение самого первого метода сборки легендарного кубика 3х3х3. Сейчас же освоить сборку головоломки можно за 20 минут с любого случайного видео из интернета… Более того, я насчитал более 20-ти разных методов сборки для обычного куба 3х3х3!

3.У Рубика не сразу получилось придумать то, что так привычно нам сейчас. Одними из первых моделей были 27 кубиков, стянутые резинками, но эта модель провалилась. В конечном итоге решение пришло профессору на реке: он придумал, как сцепить все детали за счет внутренней формы деталей (по крайней мере так гласят древние скрижали египтян… ладно, просто так гласит история)

4.Своей популярности Рубик обязан случаю, так как один из его будущих знакомых, компьютерный предприниматель Тибор Лаци, заинтересовался игрушкой, просто зайдя в кафе и увидев её у официанта («Египетские свитки» гласят и об этом). После именно этот человек связал два конца судьбы головоломки: профессора-изобретателя и попсовость кубика и его массовое производство.

Но хватит истории (к черту и египтян) … Что же именно пытался объяснить студентам Рубик? Зачем действительно был создан кубик Рубика? Тут нужен небольшой математический экскурс. Не бойтесь, я расскажу все на понятном языке даже 5-ти-класснику (по крайней мере, мой брат 5-классник понял, прочитав статью еще перед её публикацией), на примере абстрактных оранжевых псевдокрокодилов =)

Теория Групп сидит чуть ли ни на каждой веточке математики. Скажем просто: она обобщает. Числа, функции, точки на плоскости, - все. По определению группа – это

1)      Некое множество элементов, которые можно переставлять друг с другом при помощи одной операции (например, пятнашки, которые можно сдвигать),

2)      Все перестановки, произведенные с помощью операции группы над любыми её элементами ведут в неё саму.

То есть, грубо говоря, невозможно сделать такие повороты на кубике, чтобы перевернулась только одна деталька – это известно любому начинающему спидкуберу. Дайте угадаю, вы тоже разыгрывали своих друзей, переставляя или вращая детальки так, чтобы куб в конце не собрался? Дело все как раз в том, что такое перемещение выводит куб из его начальной группы, поэтому группа – это когда все перестановки ведут в неё саму.

3)      Операция ассоциативна

4)      Присутствует нейтральный элемент

5)      И каждому элементу есть обратный.

А теперь по-человечески. У нас есть один оранжевый псевдокрокодил. У него есть ноги. Как правило, у крокодилов, пусть и у оранжевых по четыре ноги. Мы не будем уходить от этого обыкновения.

Теперь нам нужна операция. За операцию я возьму пришивание к одной лапе оранжевого псевдокрокодила еще одного такого же при том, что размер пришиваемого крокодила равен размеру ноги предыдущего, к которому пришиваем (псевдокрокодилы уменьшаются при сшивании).

У нас есть множество ног и операция (сшивание). Теперь нам нужна какая-то ассоциативность операции, какой-то непонятный нейтральный элемент и чего-то на счет обратности. Обо всем по порядку.

 Ассоциативность – это то, что известно даже ученику начальной школы, только он не знает об этом. Все равно, что назвать воду гидроксидом водорода или монооксидом дигидрогена. Проще говоря, ассоциативность — это обычное свойство вида.

А*(В*С) = (А*B) *C

Касательно наших псевдокрокодилов это звучало бы так: «неважно в каком порядке что мы будем делать: сперва пришивать к каждой ноге среднего крокодила еще по одному маленькому, а потом четыре таких средних к одному большому, или сперва к большому 4 средних, а к ним еще по 4 маленьких, - все равно у нас будет одна и так же крокозябра. Можете проверить сами в следующий раз, когда встретите 21-ого крокодила с четырьмя лапами. Вот если бы от порядка пришивания что-то менялось – такая невероятная анатомическая структура псевдокрокодилов не была бы группой… да-да, в математике и такое бывает»

Теперь что такое «нейтральный крокодил». Нейтральный – это такой, который при сшивании с чем-угодно аннигилирует, то есть… не хочет ни с кем сшиваться, трусливо поглощает самого себя с хвоста, прячется внутрь и исчезает, оставляя только того, с кем его сшивали. А обратный – это такой крокодил, при сшивании которого с каким-то другим получается нейтральный псевдокрокодил. Например, если 0 – это нейтральный псевдокрокодил, то любые числа вроде 1 и -1, или 2 и -2, или 3 и -3… обратны друг другу, так как дают при сшивании нейтрального. На самом деле все чуточку сложнее, но на поверхностном интуитивном уровне можно представлять это так.

Так вот, оказывается, кубик – это идеальная демонстрация «сшивания оранжевых псевдокрокодилов» в контексте математики. Состояния кубика – это элементы группы, а переход от одного состояния другому – это операция. Если изучить свойства такой операции, то есть «сшивания крокодилов в одного длинного крокодильего крокодила», с точки зрения нейтральных и обратных элементов, можно обнаружить много всего интересного.

И есть еще пара математических фокусов, о которых я не могу не сказать в такой интересной статье.

Не обращали ли вы внимания на то, что, если повторять одну и ту же комбинацию, она обязательно приведет в начальное состояние? Здесь есть одна очень грубая ошибка. Некоторые спидкуберы видят, как кто-то повторяет одни и те же движения из собранного кубика, и в конце он собирается. Еще хуже, когда вы подошли в компанию друзей не сразу, а когда половина повторений уже была сделана. И тогда вы делаете логичный, но совершенно ошибочный вывод: если крутить одинаково, куб обязательно соберется.

Почему это не так?.. Потому что на самом деле куб не должен собираться – он всего лишь возвращается в то положение, с которого вы начали. И это состояние совершенно не обязательно собранное! Проще говоря, если начали из собранного – будет собранный, если нет – то нет.

Но в чем же фокус? Я могу научить вас, как найти количество таких повторений, даже не вращая кубик (или не вращая до конца)! Все очень просто: надо проследить за траекторией каждой детальки, и посмотреть, за сколько ходов она вернется на место (Важно! Деталька должна приходить на место в той же ориентации, не повернутой). После этого, когда такие числа найдены для всех деталек, надо просто найти Наименьшее Общее Кратное всех этих чисел – и вуаля, можно идти и удивлять друзей :)

Попробуйте, например, найти Наименьшее Общее Кратное для одной такой комбинации: RU? А потом подтвердите на практике.

И есть последняя вещь, которой я хотел бы коснуться. Это паритеты. На самом деле, нам снова надо вернуться к истории создания кубика Рубика и истории (ох уж эти Египтяне). Понятие паритета на самом деле пришло именно из Теории Групп. Уже потом спидкуберы растащили его на запчасти.

Паритетом в спидкубинге, например, считаются вот такие ситуации:

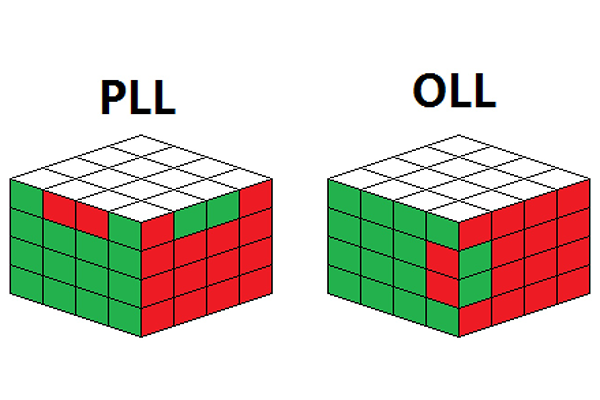
Но почему они изначально стали так называться?..

Пусть у нас есть некая группа оранжевых псевдокрокодилов, и в ней, как мы уточняли в начале, все перестановки должны вести в неё же. А мы возьмем, и сделаем такую группу, что это будет не так. Можем так сделать? Конечно можем – математика для того и создана, чтобы изучать то, чего не может быть.

Вот, например, если мы будет сводить кубик 4х4х4 редукцией (см. предыдущие статьи: https://cubemarket.ru/blog/novyj-spidkubing-bandazhi-statya-2) к кубику 3х3х3, у нас как раз и возникнет такая ситуация, когда обычными формулами 3х3х3 это не собрать. То есть, говоря научным, но простым языком, «мы выбились из группы». И вот такие «выбивания» и называются паритетами. Это может быть вообще любая ситуация, в зависимости от того, какую группу мы брали изначально. Например:

1.На Void кубе (Есть в магазине: https://cubemarket.ru/products/rubiks-void-cube) может быть ситуация, невозможная на трешке, так как в группу больше не входят центральные элементы.

2.Если собирать куб чисто пиф-пафами, будет паритет, как pll на кубике 4х4 (проверьте сами - попробуйте)

3.Если вообще взять повороты только двух сторон кубика, паритетами будут все ситуации, которые не собираются этими гранями.

4.На некоторых бандажных кубах это тоже имеет место, так как там есть ограничения свободы действий (см. https://cubemarket.ru/blog/novyj-spidkubing-bandazhi-statya-1)

Вот и все. Обогатились? – вперед удивлять друзей ;)